Shortest Addition Chain Algorithm

Now we focus on the shortest addition chains. 36 rows Shortest Addition Chains.

Addition Chains

A graphics processing unit GPU has been widely used to accelerate discrete optimization problems.

Shortest addition chain algorithm. Here are the sums that make it an addition chain. To be more precise any chain length is equal to log 2n plus the number of small steps. The first example of where it does better is for a 15 displaystyle a15 where the binary method needs six multiplies but a shortest addition chain requires only five.

Introduction A finite sequence of positive integers a 0 a 1 a. Trivially the shortest chain for any number nmust have at least log 2n steps. λ ai λ ai-1 1 and we call this a large step.

The computational aspects of finding the shortest addition chains for an integer are investigated in this work. It is extremely popular. Brauers algorithm is often called the left-to-right 2k-ary method or simply 2k-ary method.

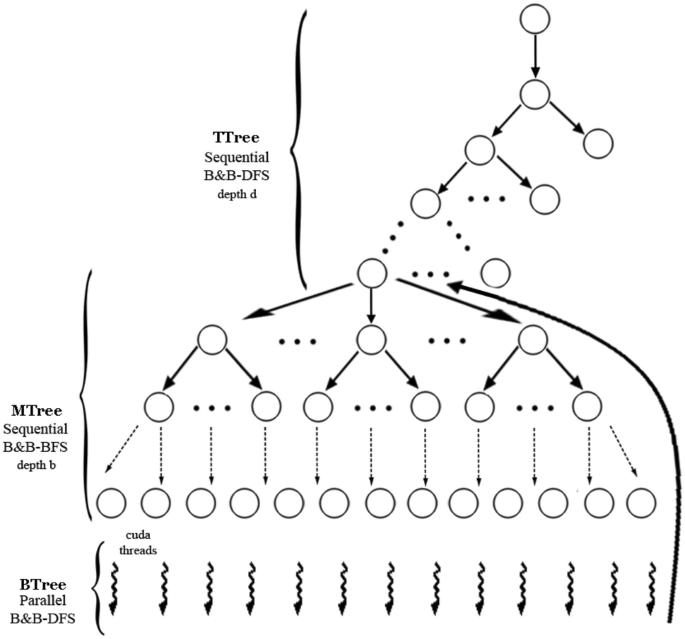
In this paper we introduce a novel hybrid parallel algorithm to generate a shortest addition chain for a positive integer e. If ai2ai-1 is called a doubling. The main idea of the proposed algorithm is to divide the search tree into a sequence of three subtrees.

S n l n - λ n For step i of an addition chain we have two possibilities. Top middle and bottom. 1 1 2 1 2 3 1 3 4 3 4 7 1 7 8 8 8 16 16 16 32 7 32 39 32 39 71 In this challenge you will be given a positive integer n and you must output one of the shortest addition chains which ends in n.

Hugo Pfoertner Addition chains Kari Ragnarsson Bridget Eileen Tenner Obtainable Sizes of Topologies on Finite Sets Oct 06 2008 Journal of Combinatorial Theory Series A 117 2010 138-151. Our experimental results show that compared to the fastest sequential algorithm for generating a shortest addition chain we improve the generation by about 70 using one. When n 9 then there are at least four small steps in any chain for ex-ponent length n.

The length of an addition chain is bounded below by log 2 e log 2 He 213 and so a shorter addition chain for e is not to be found cf. Jorge Olivos On vectorial addition chains J. Brauer chain is a sac for n 12509.

λ ai λ ai-1 and we call this a small step. Scho or Knut Section 463 Exercises 28 29. A star chain aka Brauer chain is an addition chain where ih-1 ie.

Now we focus on the shortest addition chains. Let n be the number of ones in the binary representation of the exponent n. Theoretically developed lower and upper bounds for the minimal length of the addition.

Due to the non-polynomial time required for generating a shortest AC several algorithms have been proposed to find a short. For our example this means that the shortest addition chain for e 123 has length at least 8 and so the results of the M -ary methods cited earlier seem not to be the best possible. For example in the shortest addition chain for a 15 the subproblem for a 6 must be computed as a 3 2 since a 3 is re-used as opposed to say a 6 a 2 a 2 2 which also requires three multiplies.

To be more precise any chain length is equal to log 2n plus the number of small steps 2. Trivially the shortest chain for any number nmust have at least log 2n steps. The second main step is computing the addition chain for 2n-1 The minimal length addition chain for 2n-1 is 1 2 4 ldots 2n-1 It can be computed by using the prefix-product algorithm on A0n-1 and n2log log n processors as follows.

Algorithms 2 1981 13-21. A Brauer chain aka star-chain is an addition chain where each new element is formed as the sum of the previous element and some element possibly the same. The shortest addition-chain algorithm requires no more multiplications than binary exponentiation and usually less.

V n number of 1s in the binary representation of n. Again for step i we say that. An addition chain AC is one of the strategies used to reduce the time consumed by ME through generating a shortestshort chain.

A strictly monotonically increasing shortest addition chain sac for n is an addition chain such that no shorter addition chain for n exists and a_i1 a_i for all i 1dotsk-1.

Project Euler 122 Most Efficient Exponentiation Method Mathblog